Ze względu na majoiwą awarię Portalu termin wysyłania rozwiązań został przedłużony do 10 VI.
Zad. 1. Trapez prostokątny podzielono dwiema prostymi równoległymi do podstaw na trzy trapezy o jednakowych wysokościach i polach równych odpowiednio 1, 2 i 3. Oblicz stosunek długości podstaw wyjściowego trapezu.
Zad. 2. Czy istnieje wielościan mający tyle samo krawędzi co przekątnych? Jeśli tak, podaj przykład. Jeśli nie, uzasadnij dlaczego.
Zad. 3. Z pewnych dwudziestu różnych liczb całkowitych utworzono 10 par – każda o sumie 10. Uzasadnij, że wśród tych dwudziestu liczb są dwie, których różnica jest większa od 19.
W maju punkty zdobyli:
- 2,5 – Paweł Prasal III LO Leszno, Gabriela Pułecka V LO Wrocław, Cezary Rębiś ZSE Radom, Zuzanna Czapiewska ZSB Słupsk;
- 2,25 – Miłosz Zakrzewski LO Tuchola,
- 1,5 – Artur Bumażnik ZSE Jelenia Góra, Emilia Cichowska II LO Lubin, Jagoda Janiś LO Góra,
Pozostali uczestnicy otrzymali poniżej 1 punktu.
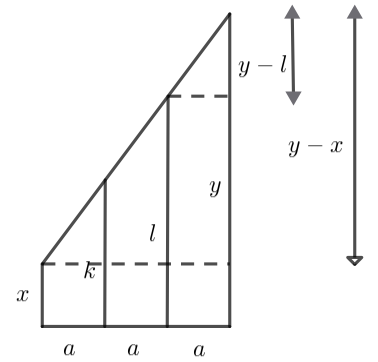
Zad. 1. Oznaczmy podstawy otrzymanych trapezów przez x, k, l, y. Na podstawie podobieństwa trójkątów (rysunek niżej) otrzymujemy proporcje: (k–x)/a = (y–x)/3a oraz y–l/a = (y–x)/3a, skąd otrzymujemy odpowiednio: k = x+(y–x)/3 = (2x+y)/3 i l = y–(y–x)/3 = (2y+x)/3. Z zależności między polami wynika, że 2.(x+k)/2.a = (k+l)/2.a, skad 2x = l–k. Po podstawieniu za l i k otrzymujemy 2x = (2y+x)/3–(2x+y)/3, skąd y/x=7.
Zad. 2. Oznaczmy jako n liczbę wierzchołków jednej podstawy graniastosłupa, n≥3. Wówczas liczba wszystkich krawędzi graniastosłupa wynosi 3n. Z każdego wierzchołka można wyprowadzić n–3 przekątne bryły biegnące do wierzchołków przeciwległej podstawy. Wszystkich przekątnych jest więc n(n–3). Zgodnie z warunkami zadania otrzymujemy równanie n(n–3) = 3n, skąd n=0 lub n=6. Ponieważ n≥3, więc n=6. Zatem graniastosłup sześciokątny ma 3.6=18 krawędzi i 6.(6–3)=18 przekątnych.
Zad. 3. Uporządkujmy dane liczby rosnąco. Rozstęp jest najmniejszy, gdy są to kolejne liczby całkowite i wynosi w tym przypadku (k+19)–k=19. Przypuśćmy, że istnieje 20 kolejnych liczb całkowitych, z których można utworzyć 10 par dających sumy 10. Oznaczmy je jako: k, k+1, k+2, …, k+19. Obliczmy sumę tych liczb na dwa sposoby. Z jednej strony jest ona równa 10.10, z drugiej - 20k+(1+2+3+..+19) = 20k+190. Otrzymujemy równość 20k+190 = 100, czyli k =-4,5. Otrzymana sprzeczność obala przypuszczenie. Po uporządkowaniu musimy otrzymać liczby, których rozstęp będzie większy niż 19.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
